Mandy Gu on Word Embeddings and Text Classification – The Central Equilibrium – Episode 9

I am so grateful to Mandy Gu for being a guest on The Central Equilibrium to talk about word embeddings and text classification.  She began by showing how data from text can be encoded in vectors and matrices, and then she used a naive Bayes classifier to classify sentences as toxic or non-toxic – a very common problem for moderating discussions in online forums.  I learned a lot from her in this episode, and you can learn more from Mandy on her Medium blog.

If you are not familiar with naive Bayes classifiers, then I encourage you to watch my video tutorial about this topic first.

Mitchell Boggs on Game Theory in Behavioural Ecology – The Central Equilibrium – Episode 8

Mitchell Boggs kindly talked about game theory in behavioural ecology on my talk show, “The Central Equilibrium”!  He talked about 2 key examples:

• when animals choose to share or fight for food
• when parents choose to care for their offspring or seek new mates to produce more offspring

These examples illustrate why seemingly disadvantageous behaviours can persist or even dominate in the animal kingdom.

Mitch recommends a book called “Are We Smart Enough to Know How Smart Animals Are?” by Frans de Waal.

Thanks for being such a great guest, Mitchell!

David Veitch on Rational vs. Irrational Numbers and Countability – The Central Equilibrium – Episode 7

I am so grateful that David Veitch appeared on my talk show, “The Central Equilibrium“, to talk about rational vs. irrational numbers.  While defining irrational numbers, he proved that is an irrational number.  He then talked about the concept of bijections while defining countability, and he showed that rational numbers are countable.

David used to work as a bond trader for Bank of America.  He writes a personal blog, and you can follow him on Twitter (@daveveitch).  He recently earned admission into the Master of Science program in statistics at the University of Toronto, and he will begin that program soon.  Congratulations, David!  Thanks for being a guest on my show!

Part 1

 

Part 2

Arnab Chakraborty on The Monty Hall Problem and Bayes’ Theorem – The Central Equilibrium – Episode 6

I am pleased to welcome Arnab Chakraborty back to my talk show, “The Central Equilibrium“, to talk about the Monty Hall Problem and Bayes’ theorem.  In this episode, he shows 2 solutions to this classic puzzle in probability, and invokes Bayes’ Theorem for the second solution.

If you have not watched Arnab’s first episode on Bayes’ theorem, then I encourage you to do that first.

Marilyn Vos Savant provided a solution to this problem in PARADE Magazine in 1990-1991.  Thousands of readers disagreed with her solution and criticized her vehemently (and incorrectly) for her error.  Some of these critics were mathematicians!  She included some of those replies and provided alternative perspectives that led to the same conclusion.  Although I am dismayed by the disrespect that some people showed in their letters to her, I am glad that a magazine column on probability was able to attract so much readership and interest.  Arnab and I referred to one of her solutions in our episode.  Thank you, Marilyn!

Enjoy this episode of “The Central Equilibrium“!

Benjamin Garden on Simple vs. Compound Interest in Finance – The Central Equilibrium – Episode 5

I am so pleased to publish this new episode of “The Central Equilibrium“, featuring Benjamin Garden.  He talked about simple and compound interest in the context of finance and investment, highlighting the power of compound interest to grow your money and to enlarge debt from credit cards.  We compared the formulas for calculating the accrued amounts under simple and compound interest, and we derived the formula for the Rule of 72, a short-cut to estimate the length of time needed to double your investment under compound interest.

Check out Ben’s blog, Twitter account (@GardenBenjamin), and Instagram account (@ben.garden) to get more advice about managing your money!

Part 1:

 

Part 2:

Layne Newhouse on representing neural networks – The Central Equilibrium – Episode 4

I am excited to present the first of a multi-episode series on neural networks on my talk show, “The Central Equilibrium”.  My guest in this series in Layne Newhouse, and he talked about how to represent neural networks. We talked about the biological motivations behind neural networks, how to represent them in diagrams and mathematical equations, and a few of the common activation functions for neural networks.

Check it out!

Video Tutorial – The Moment Generating Function of the Exponential Distribution

In this video tutorial on YouTube, I derive the moment generating function (MGF) of the exponential distribution.  Visit my YouTube channel to watch more video tutorials!

Arnab Chakraborty on Bayes’ Theorem – The Central Equilibrium – Episode 3

Arnab Chakraborty kindly came to my new talk show, “The Central Equilibrium”, to talk about Bayes’ theorem.  He introduced the concept of conditional probability, stated Bayes’ theorem in its simple and general forms, and showed an example of how to use it in a calculation.

Check it out!

Christopher Salahub on Markov Chains – The Central Equilibrium – Episode 2

It was a great pleasure to talk to Christopher Salahub about Markov chains in the second episode of my new talk show, The Central Equilibrium!  Chris graduated from the University of Waterloo with a Bachelor of Mathematics degree in statistics.  He just finished an internship in data development at Environics Analytics, and he is starting a Master’s program in statistics at ETH Zurich in Switzerland.

Chris recommends “Introduction to Probability Models” by Sheldon Ross to learn more about probability theory and Markov chains.

The Central Equilibrium is my new talk show about math, science, and economics. It focuses on technical topics that involve explanations with formulas, equations, graphs, and diagrams.  Stay tuned for more episodes in the coming weeks!

You can watch all of my videos on my YouTube channel!

Please watch the video on this blog.  You can also watch it directly on YouTube.

Neil Seoni on the Fourier Transform and the Sampling Theorem – The Central Equilibrium – Episode 1

I am very excited to publish the very first episode of my new talk show, The Central Equilibrium!  My guest is Neil Seoni, an undergraduate student in electrical and computer engineering at Rice University in Houston, Texas. He has studied data science in his spare time, most notably taking a course on machine learning by Andrew Ng on Coursera. He is finishing his summer job as a Data Science Intern at Environics Analytics in Toronto, Ontario.

Neil recommends reading Don Johnson’s course notes from Rice University and his free text book to learn more about the topics covered in his episode.

The Central Equilibrium is my new talk show about math, science, and economics. It focuses on technical topics that involve explanations with formulas, equations, graphs, and diagrams.  Stay tuned for more episodes in the coming weeks!

You can watch all of my videos on my YouTube channel!

Please watch the video on this blog.  You can also watch it directly on YouTube.

A Comprehensive Guide for Public Speaking at Scientific Conferences

Introduction

I served as a judge for some of the student presentations at the 2016 Canadian Statistics Student Conference (CSSC).  The conference was both a learning opportunity and a networking opportunity for statistics students in Canada.  The presentations allowed the students to share their research and course projects with their peers, and it was a chance for them to get feedback about their work and learn new ideas from other students.

Unfortunately, I found most of the presentations to be very bad – not necessarily in terms of the content, but because of the delivery.  Although the students showed much earnestness and eagerness in sharing their work with others, most of them demonstrated poor competence in public speaking.

Public speaking is an important skill in knowledge-based industries, so these opportunities are valuable experiences for anybody to strengthen this skill.  You can learn it only by doing it many times, making mistakes, and learning from those mistakes.  Having delivered many presentations, learned from my share of mistakes, and received much praise for my seminars, I hope that the following tips will help anyone who presents at scientific conferences to improve their public-speaking skills.  In fact, most of these tips apply to public speaking in general.

I spoke at the 2016 Canadian Statistics Student Conference on career advice for students and new graduates in statistics.

Image courtesy of Peter Macdonald on Flickr.

Mathematical Statistics Lesson of the Day – Basu’s Theorem

Today’s Statistics Lesson of the Day will discuss Basu’s theorem, which connects the previously discussed concepts of minimally sufficient statistics, complete statistics and ancillary statistics.  As before, I will begin with the following set-up.

Suppose that you collected data

in order to estimate a parameter .  Let be the probability density function (PDF) or probability mass function (PMF) for .

Let

be a statistics based on .

Basu’s theorem states that, if is a complete and minimal sufficient statistic, then is independent of every ancillary statistic.

Establishing the independence between 2 random variables can be very difficult if their joint distribution is hard to obtain.  This theorem allows the independence between minimally sufficient statistic and every ancillary statistic to be established without their joint distribution – and this is the great utility of Basu’s theorem.

However, establishing that a statistic is complete can be a difficult task.  In a later lesson, I will discuss another theorem that will make this task easier for certain cases.

Mathematical Statistics Lesson of the Day – An Example of An Ancillary Statistic

Consider 2 random variables, and , from the normal distribution , where is unknown.  Then the statistic

has the distribution

.

The distribution of does not depend on , so is an ancillary statistic for .

Note that, if is unknown, then is not ancillary for .

Eric’s Enlightenment for Friday, May 8, 2015

1. A nice set of tutorials on Microsoft Excel at OfficeTuts by Tomasz Decker.
2. “We had proved that an assertion was indeed true in all of the difficult cases, but it turned out to be false in the simple case. We never bothered to check.”  Are mistakes in academic mathematics being effectively identified and corrected?  Vladimir Voevodsky (2002 Fields Medalist) published a major theorem in 1990, but Carlos Simpson found an error with the theorem in 1998.  It wasn’t until 2013 that Voevodsky finally became convinced that his theorem was wrong.  This motivated him to develop “proof assistants” – computer programs that help to prove mathematical theorems.
3. Synthesizing artificial muscles from gold-plated onion skins
4. Andrew Gelman debriefs his presentation to Princeton’s economics department about unbiasedness and econometrics.

Mathematical Statistics Lesson of the Day – Minimally Sufficient Statistics

In using a statistic to estimate a parameter in a probability distribution, it is important to remember that there can be multiple sufficient statistics for the same parameter.  Indeed, the entire data set, , can be a sufficient statistic – it certainly contains all of the information that is needed to estimate the parameter.  However, using all variables is not very satisfying as a sufficient statistic, because it doesn’t reduce the information in any meaningful way – and a more compact, concise statistic is better than a complicated, multi-dimensional statistic.  If we can use a lower-dimensional statistic that still contains all necessary information for estimating the parameter, then we have truly reduced our data set without stripping any value from it.

Our saviour for this problem is a minimally sufficient statistic.  This is defined as a statistic, , such that

1. is a sufficient statistic
2. if  is any other sufficient statistic, then there exists a function such that

Note that, if there exists a one-to-one function such that

then  and  are equivalent.

Mathematics and Mathematical Statistics Lesson of the Day – Convex Functions and Jensen’s Inequality

Consider a real-valued function that is continuous on the interval , where and are any 2 points in the domain of .  Let

be the midpoint of and .  Then, if

then is defined to be midpoint convex.

More generally, let’s consider any point within the interval .  We can denote this arbitrary point as

where .

Then, if

then is defined to be convex.  If

then is defined to be strictly convex.

There is a very elegant and powerful relationship about convex functions in mathematics and in mathematical statistics called Jensen’s inequality.  It states that, for any random variable with a finite expected value and for any convex function ,

.

A function is defined to be concave if is convex.  Thus, Jensen’s inequality can also be stated for concave functions.  For any random variable with a finite expected value and for any concave function ,

.

In future Statistics Lessons of the Day, I will prove Jensen’s inequality and discuss some of its implications in mathematical statistics.

Mathematical Statistics Lesson of the Day – The Glivenko-Cantelli Theorem

In 2 earlier tutorials that focused on exploratory data analysis in statistics, I introduced

• the conceptual background behind empirical cumulative distribution functions (empirical CDFs)
• how to plot  empirical cumulative distribution functions in 2 different ways in R

There is actually an elegant theorem that provides a rigorous basis for using empirical CDFs to estimate the true CDF – and this is true for any probability distribution.  It is called the Glivenko-Cantelli theorem, and here is what it states:

Given a sequence of independent and identically distributed random variables, ,

In other words, the empirical CDF of converges uniformly to the true CDF.

My mathematical statistics professor at the University of Toronto, Keith Knight, told my class that this is often referred to as “The First Theorem of Statistics” or the “The Fundamental Theorem of Statistics”.  I think that this is a rather subjective title – the central limit theorem is likely more useful and important – but Page 261 of John Taylor’s An introduction to measure and probability (Springer, 1997) recognizes this attribution to the Glivenko-Cantelli theorem, too.

Mathematical Statistics Lesson of the Day – Chebyshev’s Inequality

The variance of a random variable is just an expected value of a function of .  Specifically,

.

Let’s substitute into Markov’s inequality and see what happens.  For convenience and without loss of generality, I will replace the constant with another constant, .

Now, let’s substitute with , where is the standard deviation of .  (I can make this substitution, because is just another constant.)

This last inequality is known as Chebyshev’s inequality, and it is just a special version of Markov’s inequality.  In a later Statistics Lesson of the Day, I will discuss the motivation and intuition behind it.  (Hint: Read my earlier lesson on the motivation and intuition behind Markov’s inequality.)

Mathematical Statistics Lesson of the Day – Markov’s Inequality

Markov’s inequality is an elegant and very useful inequality that relates the probability of an event concerning a non-negative random variable, , with the expected value of .  It states that

where .

I find Markov’s inequality to be beautiful for 2 reasons:

1. It applies to both continuous and discrete random variables.
2. It applies to any non-negative random variable from any distribution with a finite expected value.

In a later lesson, I will discuss the motivation and intuition behind Markov’s inequality, which has useful implications for understanding a data set.

Mathematics and Applied Statistics Lesson of the Day – The Geometric Mean

Suppose that you invested in a stock 3 years ago, and the annual rates of return for each of the 3 years were

• 5% in the 1st year
• 10% in the 2nd year
• 15% in the 3rd year

What is the average rate of return in those 3 years?

It’s tempting to use the arithmetic mean, since we are so used to using it when trying to estimate the “centre” of our data.  However, the arithmetic mean is not appropriate in this case, because the annual rate of return implies a multiplicative growth of your investment by a factor of , where is the rate of return in each year.  In contrast, the arithmetic mean is appropriate for quantities that are additive in nature; for example, your average annual salary from the past 3 years is the sum of last 3 annual salaries divided by 3.

If the arithmetic mean is not appropriate, then what can we use instead?  Our saviour is the geometric mean, 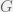.  The average factor of growth from the 3 years is

,

where is the rate of return in year 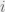, .  The average annual rate of return is .  Note that the geometric mean is NOT applied to the annual rates of return, but the annual factors of growth.

 

Returning to our example, our average factor of growth is

.

Thus, our annual rate of return is .

 

Here is a good way to think about the difference between the arithmetic mean and the geometric mean.  Suppose that there are 2 sets of numbers.

1. The first set, , consists of your data , and this set has a sample size of .
2. The second, ,  set also has a sample size of , but all values are the same – let’s call this common value .

• What number must be such that the sums in and are equal?  This value of is the arithmetic mean of the first set.
• What number must  be such that the products in and are equal?  This value of is the geometric mean of the first set.

Note that the geometric means is only applicable to positive numbers.