Eric’s Enlightenment for Friday, May 22, 2015

1. John Urschel (academically published mathematician and NFL football player) uses logistic regression, expected value and variance to anticipate that the new farther distance for the extra-point conversion will not reduce its use in the NFL.
2. John Ioannidis is widely known for his 2005 paper “Why most published research findings are false“.  In 2014, he wrote another paper on the same topic called “How to Make More Published Research True“.
3. Yoshitaka Fujii holds the record for the number of retractions of academic publications for a single author: 183 papers, or “roughly 7 percent of all retracted papers between 1980 and 2011”.
4. The chemistry of why bread stales, and how to slow retrogradation.

Performing Logistic Regression in R and SAS

Introduction

My statistics education focused a lot on normal linear least-squares regression, and I was even told by a professor in an introductory statistics class that 95% of statistical consulting can be done with knowledge learned up to and including a course in linear regression.  Unfortunately, that advice has turned out to vastly underestimate the variety and depth of problems that I have encountered in statistical consulting, and the emphasis on linear regression has not paid dividends in my statistics career so far.  Wisdom from veteran statisticians and my own experience combine to suggest that logistic regression is actually much more commonly used in industry than linear regression.  I have already started a series of short lessons on binary classification in my Statistics Lesson of the Day and Machine Learning Lesson of the Day.    In this post, I will show how to perform logistic regression in both R and SAS.  I will discuss how to interpret the results in a later post.

The Data Set

The data set that I will use is slightly modified from Michael Brannick’s web page that explains logistic regression.  I copied and pasted the data from his web page into Excel, modified the data to create a new data set, then saved it as an Excel spreadsheet called heart attack.xlsx.

• In R, I imported it using the “XLConnect” package.
• In SAS, I imported it using PROC IMPORT.

This data set has 3 variables (I have renamed them for convenience in my R programming).

1. ha2  – Whether or not a patient had a second heart attack.  If ha2 = 1, then the patient had a second heart attack; otherwise, if ha2 = 0, then the patient did not have a second heart attack.  This is the response variable.
2. treatment – Whether or not the patient completed an anger control treatment program.
3. anxiety – A continuous variable that scores the patient’s anxiety level.  A higher score denotes higher anxiety.

Read the rest of this post to get the full scripts and view the full outputs of this logistic regression model in both R and SAS!

Machine Learning and Applied Statistics Lesson of the Day – How to Construct Receiver Operating Characteristic Curves

A receiver operating characteristic (ROC) curve is a 2-dimensional plot of the (the true positive rate) versus (1 minus the true negative rate) of a binary classifier while varying its discrimination threshold.  In statistics and machine learning, a basic and popular tool for binary classification* is logistic regression, and an ROC curve is a useful way to assess the predictive accuracy of the logistic regression model.

To illustrate with an example, let’s consider the Bernoulli response variable 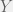and the covariates .  A logistic regression model takes the covariates as inputs and returns .  You as the user of the model must decide above which value of you will predict that ; this value is the discrimination threshold.  A common threshold is .

Once you finish fitting the model with a training set, you can construct an ROC curve by following these steps below:

1. Set a discrimination threshold.
2. Use the covariates to predict 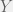for each observation in a validation set.
3. Since you have the actual response values in the validation set, you can then calculate the sensitivity and specificity for your logistic regression model at that threshold.
4. Repeat Steps 1-3 with a new threshold.
5. Plot the values of  versus for all thresholds.  The result is your ROC curve.

The use of a validation set to assess the predictive accuracy of a model is called validation, and it is a good practice for supervised learning.  If you have another fresh data set, it is also good practice to use that as a test set to assess the predictive accuracy of your model.

Note that you can perform Steps 2-5 for the training set, too – this is often done in statistics when you don’t have many data to work with, and the best that you can do is to assess the predictive accuracy of your model on the data set that you used to fit the model.

*Strictly speaking, logistic regression is a regression technique, not a classification technique.  However, when combined with a decision rule about the probability of success, logistic regression is commonly used for binary classification.

Machine Learning Lesson of the Day – Supervised Learning: Classification and Regression

Supervised learning has 2 categories:

• In classification, the target variable is categorical.
• In regression, the target variable is continuous.

Thus, regression in statistics is different from regression in supervised learning.

In statistics,

• regression is used to model relationships between predictors and targets, and the targets could be continuous or categorical.  
• a regression model usually includes 2 components to describe such relationships:
  • a systematic component
  • a random component.  The random component of this relationship is mathematically described by some probability distribution.  
• most regression models in statistics also have assumptions about the statistical independence or dependence between the predictors and/or between the observations.  
• many statistical models also aim to provide interpretable relationships between the predictors and targets.  
  • For example, in simple linear regression, the slope parameter, , predicts the change in the target, , for every unit increase in the predictor, .

In supervised learning,

• target variables in regression must be continuous
  • categorical target variables are modelled in classification
• regression has less or even no emphasis on using probability to describe the random variation between the predictor and the target
  • Random forests are powerful tools for both classification and regression, but they do not use probability to describe the relationship between the predictors and the target.
• regression has less or even no emphasis on providing interpretable relationships between the predictors and targets.  
  • Neural networks are powerful tools for both classification and regression, but they do not provide interpretable relationships between the predictors and the target.

***The last 2 points are applicable to classification, too.

In general, supervised learning puts much more emphasis on accurate prediction than statistics.

Since regression in supervised learning includes only continuous targets, this results in some confusing terminology between the 2 fields.  For example, logistic regression is a commonly used technique in both statistics and supervised learning.  It is technically a regression technique, because it estimates a probability of success in the response variable.  However, many practitioners of machine learning refer to it as a classification technique, because they apply a decision rule to that estimated probability to make a binary classification.  Strictly speaking, logistic regression is NOT a classification technique, but you must be aware of this misnomer when communicating in this field.