Exploratory Data Analysis: Kernel Density Estimation – Conceptual Foundations

For the sake of brevity, this post has been created from the first half of a previous long post on kernel density estimation.  This first half focuses on the conceptual foundations of kernel density estimation.  The second half will focus on constructing kernel density plots and rug plots in R.

Introduction

Recently, I began a series on exploratory data analysis; so far, I have written about computing descriptive statistics and creating box plots in R for a univariate data set with missing values.  Today, I will continue this series by introducing the underlying concepts of kernel density estimation, a useful non-parametric technique for visualizing the underlying distribution of a continuous variable.  In the follow-up post, I will show how to construct kernel density estimates and plot them in R.  I will also introduce rug plots and show how they can complement kernel density plots.

 

 

But first – read the rest of this post to learn the conceptual foundations of kernel density estimation.

What is a Kernel?

Before defining kernel density estimation, let’s define a kernel.  (To my surprise and disappointment, many textbooks that talk about kernel density estimation or use kernels do not define this term.)

A kernel is a special type of probability density function (PDF) with the added property that it must be even.  Thus, a kernel is a function with the following properties

• non-negative
• real-valued
• even
• its definite integral over its support set must equal to 1

Some common PDFs are kernels; they include the Uniform(-1,1) and standard normal distributions.  Wikipedia has a list of common kernels.

What is Kernel Density Estimation?

Kernel density estimation is a non-parametric method of estimating the probability density function (PDF) of a continuous random variable.  It is non-parametric because it does not assume any underlying distribution for the variable.  Essentially, at every datum, a kernel function is created with the datum at its centre – this ensures that the kernel is symmetric about the datum.  The PDF is then estimated by adding all of these kernel functions and dividing by the number of data to ensure that it satisfies the 2 properties of a PDF:

• Every possible value of the PDF (i.e. the function, ), is non-negative.
• The definite integral of the PDF over its support set equals to 1.

Intuitively, a kernel density estimate is a sum of “bumps”.  A “bump” is assigned to every datum, and the size of the “bump” represents the probability assigned at the neighbourhood of values around that datum; thus, if the data set contains

• 2 data at x = 1.5
• 1 datum at x = 0.5

then the “bump” at x = 1.5 is twice as big as the “bump” at x = 0.5.

Each “bump” is centred at the datum, and it spreads out symmetrically to cover the datum’s neighbouring values.  Each kernel has a bandwidth, and it determines the width of the “bump” (the width of the neighbourhood of values to which probability is assigned).  A bigger bandwidth results in a shorter and wider “bump” that spreads out farther from the centre and assigns more probability to the neighbouring values.

Constructing a Kernel Density Estimate: Step by Step

1) Choose a kernel; the common ones are normal (Gaussian), uniform (rectangular), and triangular.

2) At each datum, , build the scaled kernel function

,

where is your chosen kernel function.  The parameter is called the bandwidth, the window width, or the smoothing parameter.

3) Add all of the individual scaled kernel functions and divide by ; this places a probability of to each .  It also ensures that the kernel density estimate integrates to 1 over its support set.

The density() function in R computes the values of the kernel density estimate.  Applying the plot() function to an object created by density() will plot the estimate.  Applying the summary() function to the object will reveal useful statistics about the estimate.

Choosing the Bandwidth

It turns out that the choosing the bandwidth is the most difficult step in creating a good kernel density estimate that captures the underlying distribution of the variable (Trosset, Page 166).  Choosing the bandwidth is a complicated topic that is better addressed in a more advanced book or paper, but here are some useful guidelines:

• A small results in a small standard deviation, and the kernel places most of the probability on the datum.  Use this when the sample size is large and the data are tightly packed.
• A large results in a large standard deviation, and the kernel spreads more of the probability from the datum to its neighbouring values.  Use this when the sample size is small and the data are sparse.

There is a tremendous amount of literature on how best to choose the bandwidth, and I will not go into detail about that in this post.  There are 2 methods that are common in R: nrd0 and SJ, which refers to the method by Sheather & Jones.  These are string arguments for the option ‘bw’ in the density() function.  The default in density() is bw = ‘nrd0’.

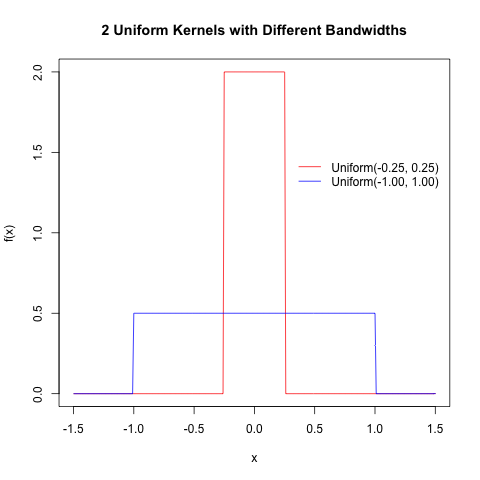
Here is some R code to generate the following plots of 2 uniform kernel functions; note the use of the dunif() function.

##### Plot 2 Uniform Kernel Functions with Different Bandwidths
##### By Eric Cai - The Chemical Statistician

# define support set of X
x = seq(-1.5, 1.5, by = 0.01)

# obtain uniform kernel function values
uniform1 = dunif(x, min = -0.25, max = 0.25)
uniform2 = dunif(x, min = -1.00, max = 1.00)

# optional printing of PNG image to chosen directory
png('INSERT YOUR DIRECTORY PATH HERE/uniform kernels.png')
plot(x, uniform1, type = 'l', ylab = 'f(x)', xlab = 'x', main = '2 Uniform Kernels with Different Bandwidths', col = 'red')

# add plot of second kernel function
lines(x, uniform2, col = 'blue')

# add legend; must specify 'lty' option, because these are line plots
legend(0.28, 1.5, c('Uniform(-0.25, 0.25)', 'Uniform(-1.00, 1.00)'), lty = c(1,1), col = c('red', 'blue'), box.lwd = 0)
dev.off()

References

Trosset, Michael W. An introduction to statistical inference and its applications with R. Chapman and Hall/CRC, 2011.

Everitt, Brian S., and Torsten Hothorn. A handbook of statistical analyses using R. Chapman and Hall/CRC, 2006.