Exploratory Data Analysis – Kernel Density Estimation and Rug Plots in R on Ozone Data in New York and Ozonopolis

Update on July 15, 2013:

Thanks to Harlan Nelson for noting on AnalyticBridge that the ozone concentrations for both New York and Ozonopolis are non-negative quantities, so their kernel density plot should have non-negative support sets.  This has been corrected in this post by

– defining new variables called max.ozone and max.ozone2

– using the options “from = 0” and “to = max.ozone” or “to = max.ozone2” in the density() function when defining density.ozone and density.ozone2 in the R code.

Update on February 2, 2014:

Harlan also noted in the above comment that any truncated kernel density estimator (KDE) from density() in R does not integrate to 1 over its support set.  Thanks to Julian Richer Daily for suggesting on AnalyticBridge to scale any truncated kernel density estimator (KDE) from density() by its integral to get a KDE that integrates to 1 over its support set.  I have used my own function for trapezoidal integration to do so, and this has been added below.

I thank everyone for your patience while I took the time to write a post about numerical integration before posting this correction.  I was in the process of moving between jobs and cities when Harlan first brought this issue to my attention, and I had also been planning a major expansion of this blog since then.  I am glad that I have finally started a series on numerical integration to provide the conceptual background for the correction of this error, and I hope that they are helpful.  I recognize that this is a rather late correction, and I apologize for any confusion.

For the sake of brevity, this post has been created from the second half of a previous long post on kernel density estimation.  This second half focuses on constructing kernel density plots and rug plots in R.  The first half focused on the conceptual foundations of kernel density estimation.

Introduction

This post follows the recent introduction of the conceptual foundations of kernel density estimation.  It uses the “Ozone” data from the built-in “airquality” data set in R and the previously simulated ozone data for the fictitious city of “Ozonopolis” to illustrate how to construct kernel density plots in R.  It also introduces rug plots, shows how they can complement kernel density plots, and shows how to construct them in R.

This is another post in a recent series on exploratory data analysis, which has included posts on descriptive statistics, box plots, violin plots, the conceptual foundations of empirical cumulative distribution functions (CDFs), and how to plot empirical CDFs in R.

Read the rest of this post to learn how to create the above combination of a kernel density plot and a rug plot!

Example: Ozone Pollution Data from New York and Ozonopolis

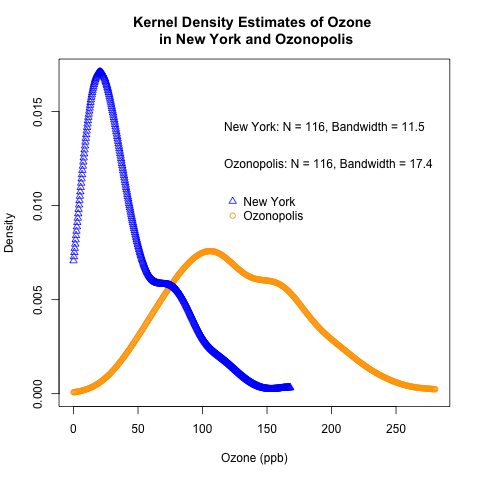
Recall that I used 2 sets of ozone data in my last post about box plots.  One came from the “airquality” data set that is built into R.  I simulated the other one and named its city of origin “Ozonopolis”.  Here are the code and the plot of the kernel density estimates (KDEs) of the 2 ozone pollution data sets.  I used the default settings in density() – specifically, I used the normal (Gaussian) kernel and the “nrd0” method of choosing the bandwidth.  I encourage you to try the other settings.  I have used the set.seed() function so that you can replicate my random numbers.

Thanks to Harlan Nelson and Julian Richer Daily, I have learned that the KDE from density() does not integrate to 1 if the support set is truncated with the “from = ” or “to = ” options.  To correct this problem, I have used trapezoidal integration to integrate the resulting KDE and divide the KDE by that integral; this scaled KDE will integrate to 1.  In my correction below, I saved the function in an R script called “trapezoidal integration.R” in my working directory, and I then called it via the source() function.

##### Kernel Density Estimation
##### By Eric Cai - The Chemical Statistician

# clear all variables in the workspace 
rm(list = ls(all.names = TRUE)) 

# set working directory
setwd('INSERT YOUR WORKING DIRECTORY PATH HERE')

# extract "Ozone" data vector for New York 
ozone = airquality$Ozone 

# calculate the number of non-missing values in "ozone" 
n = sum(!is.na(ozone)) 

# calculate mean, variance and standard deviation of "ozone" by excluding missing values 
mean.ozone = mean(ozone, na.rm = T) 
var.ozone = var(ozone, na.rm = T) 
sd.ozone = sd(ozone, na.rm = T) 
max.ozone = max(ozone, na.rm = T) 

# simulate ozone pollution data for ozonopolis 
# set seed for you to replicate my random numbers for comparison 
set.seed(1) 

ozone2 = rgamma(n, shape = mean.ozone^2/var.ozone+3, scale = var.ozone/mean.ozone+3) 
max.ozone2 = max(ozone2) 

# obtain values of the kernel density estimates 
density.ozone = density(ozone, na.rm = T, from = 0, to = max.ozone) 
density.ozone2 = density(ozone2, na.rm = T, from = 0, to = max.ozone2) 

# access function for trapezoidal integration
source('trapezoidal integration.r')

# scale the kernel density estimates by their integrals over their support sets 
kde = density.ozone$y
support.ozone = density.ozone$x 
integral.kde = trapezoidal.integration(support.ozone, kde) 
kde.scaled = kde/integral.kde 

kde2 = density.ozone2$y
support.ozone2 = density.ozone2$x 
integral.kde2 = trapezoidal.integration(support.ozone2, kde2) 
kde.scaled2 = kde2/integral.kde2 

# number of points used in density plot 
n.density1 = density.ozone$n 
n.density2 = density.ozone2$n 

# bandwidth in density plot 
bw.density1 = density.ozone$bw 
bw.density2 = density.ozone2$bw

# plot kernel density estimates and export as PNG image
png('kernel density plot ozone.png')
plot(support.ozone2, kde.scaled2, ylim = c(0, max(kde.scaled)), main = 'Kernel Density Estimates of Ozone \n in New York and Ozonopolis', xlab = 'Ozone (ppb)', ylab = 'Density', lty = 1, pch = 1, col = 'orange')
points(support.ozone, kde.scaled, pch = 2, col = 'blue')

# add legends to state sample sizes and bandwidths; notice use of paste()
legend(100, 0.015, paste('New York: N = ', n.density1, ', Bandwidth = ', round(bw.density1, 1), sep = ''), bty = 'n')
legend(100, 0.013, paste('Ozonopolis: N = ', n.density2, ', Bandwidth = ', round(bw.density2, 1), sep = ''), bty = 'n')

# add legend to label plots
legend(115, 0.011, c('New York', 'Ozonopolis'), pch = c(2,1), col = c('blue', 'orange'), bty = 'n')
dev.off()

It is clear that Ozonopolis has more ozone pollution than New York.  The right-skewed shapes of both curves also suggest that the normal distribution may not be suitable.  (If you read my blog post carefully, you will already see evidence of a different distribution!)  In a later post, I will use quantile-quantile plots to illustrate this.  Stay tuned!

To give you a better sense of why the density plots have higher “bumps” at certain places, take a look at the following plot of the ozone pollution just in New York.  Below the density plot, you will find a rug plot – a plot of tick marks along the horizontal axis indicating where the data are located.  Clearly, there are more data in the neighbourhood between 0 and 50, where the highest “bump” is located.  Use the rug() function to get the rug plot in R.

# plot KDE with rug plot and export as PNG image
png('kernel density plot with rug plot ozone New York.png')
plot(support.ozone, kde.scaled, main = 'Kernel Density Plot and Rug Plot of Ozone \n in New York', xlab = 'Ozone (ppb)', ylab = 'Density')
rug(ozone)
dev.off()

 

References

Trosset, Michael W. An introduction to statistical inference and its applications with R. Chapman and Hall/CRC, 2011.

Everitt, Brian S., and Torsten Hothorn. A handbook of statistical analyses using R. Chapman and Hall/CRC, 2006.