Detecting Unfair Dice in Casinos with Bayes’ Theorem

Introduction

I saw an interesting problem that requires Bayes’ Theorem and some simple R programming while reading a bioinformatics textbook.  I will discuss the math behind solving this problem in detail, and I will illustrate some very useful plotting functions to generate a plot from R that visualizes the solution effectively.

The Problem

The following question is a slightly modified version of Exercise #1.2 on Page 8 in “Biological Sequence Analysis” by Durbin, Eddy, Krogh and Mitchison.

An occasionally dishonest casino uses 2 types of dice.  Of its dice, 97% are fair but 3% are unfair, and a “five” comes up 35% of the time for these unfair dice.  If you pick a die randomly and roll it, how many “fives”  in a row would you need to see before it was most likely that you had picked an unfair die?”

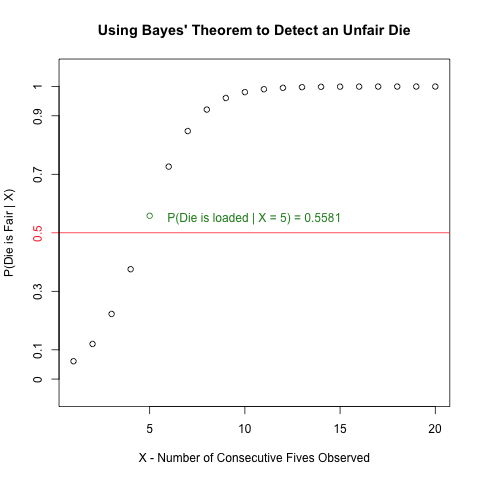
Read more to learn how to create the following plot and how it invokes Bayes’ Theorem to solve the above problem!

Translating the Problem into Math

To translate this problem into the language of probability,

• let denote the outcome of rolling any die.  The possible outcomes are .
• let denote whether the die is fair or not.  The possible outcomes are .
• let denote the number of consecutive times a “five” is observed after rolling a die.  The possible outcomes are all non-negative integers.

We know that

• 
• 
• 
• 

The die that you picked is either fair or unfair, regardless of how many times you roll the die.  Thus, given that we observe  consecutive fives, a sensible way to decide that a die is unfair is if the probability of the die being unfair given  is higher than the probability of the die being fair given .  Mathematically, we seek the value of such that

To see why this equation formulates our problem accurately, let’s assume that it is true.  Combining Equation and the fact that is a Bernoulli random variable,

and this is the premise of the question.

Using Bayes’ Theorem

To calculate , let’s use Bayes’ Theorem.  I always “work out” Bayes’ Theorem by

1. stating the definition of conditional probability,
2. applying the law of total probability.

To apply the definition of conditional probability for our problem,

.

Now, re-write the joint probability in the numerator by applying the definition of conditional probability again, but reversing the conditionality.

.

Finally, apply the law of total probability to the denominator.  (Because of the difficulties of writing LaTeX in WordPress, the entire denominator is written on the second line.  Please excuse the awkward line placement.)

By Equation , set 0.5 to be less than the above equation.

Tthe probability of getting consecutive “fives” is the joint probability of getting  individual “fives”, regardless of whether the die is fair or not.  By the independence between rolls of the die, this probability is just the product of the marginal probabilities of getting  individual “fives”.  Since these marginal probabilities are the same, it is simply that marginal probability to the power of .  Mathematically,

Plotting the Solution in R

To solve the problem, we need to find the minimum value of such that Inequality is true.  This inequality cannot be solved analytically, so I computed the right-hand side of for various possible values of in R.  Below is the resulting plot.  Many functions were used to generate it.

• plot() to generate the basic plot of points; note the use of the ifelse() function to set the unique colour for the point at
• text() to add custom text with a green colour inside the plot
• abline() to add a custom line with a brown colour
• axis() to add custom tick marks
• mtext() to add a custom tick label at 0.5 with a brown colour to the vertical axis

I encourage you to study the code carefully to learn all of the useful functions and build your own plot with custom axes, tick marks, and tick labels.

Notice that I needed to use the axis() function twice to add all of the tick marks that I wanted.  For some reason, I could not add ‘0’ and ‘1’ among the first set of tick marks, but I could add them separately in a second calling of axis().

I also found a document by Tian Zheng from Columbia University that lists the names of various colours in R.  It turns out that there are many more colours than the standard ones that I usually use from the colours of a rainbow!

As the plot shows, if you see 5 or more consecutive “fives”, you have reason to suspect that the die is unfair.

##### Detecting an Unfair Die with Bayes' Theorem
##### By Eric Cai - The Chemical Statistician

# set the possible values of the number of consecutive "fives" observed from rolling a die
x = 1:20

# calculate the probability of the die being unfair given the observed number of consecutive "fives"
prob.loaded = (0.35^x)*0.03/((0.35^x)*0.03 + ((1/6)^x)*0.97)

# export the plot as a PNG image file
png('INSERT YOUR DIRECTORY PATH HERE/unfair die plot.png')

# plot the calculated probabilities
# notice that the "yaxt = 'n'" option suppresses the verticle axis; I want to add my own custom axis later
plot(x, prob.loaded, col=ifelse(x == 5, "forestgreen", "black"), ylab = 'P(Die is Fair | X)', ylim = c(-0.05, 1.05), xlab = 'X - Number of Consecutive Fives Observed', yaxt='n', main = "Using Bayes' Theorem to Detect an Unfair Die")

# add a custom horizontal line to show where P(Die = Unfair | X = x) = 0.5
abline(0.5, 0, col = 'firebrick1')

# add a custom tick mark with the colour 'firebrick1'
# the label is left intentionally blank, because its colour can only be black
# use mtext() to set the tick label's colour
axis(2, at = c(0.5), col = 'firebrick1', labels = ' ')

# add a custom tick label at P(Die = Unfair | X = x) = 0.5
# distinguish it with the colour 'firebrick1'
mtext(text = '0.5', side = 2, line = 1, col = "firebrick1")

# add text to denote the point of interest
text(9, 0.55, 'P(Die is loaded | X = 5) = 0.5581', col = 'forestgreen')

# add some other tick marks to show the other values along the vertical axis
axis(2, at = c(0.1, 0.3, 0.7, 0.9), labels = c('0.1', '0.3', '0.7', '0.9'))
axis(2, at = c(0, 1), labels = c('0', '1'))

dev.off()

Reference

Durbin, R. (Ed.). (1998). Biological sequence analysis: probabilistic models of proteins and nucleic acids. Cambridge university press.