Video Tutorial – Obtaining the Expected Value of the Exponential Distribution Using the Moment Generating Function

In this video tutorial on YouTube, I use the exponential distribution’s moment generating function (MGF) to obtain the expected value of this distribution.  Visit my YouTube channel to watch more video tutorials!

Eric’s Enlightenment for Friday, May 22, 2015

1. John Urschel (academically published mathematician and NFL football player) uses logistic regression, expected value and variance to anticipate that the new farther distance for the extra-point conversion will not reduce its use in the NFL.
2. John Ioannidis is widely known for his 2005 paper “Why most published research findings are false“.  In 2014, he wrote another paper on the same topic called “How to Make More Published Research True“.
3. Yoshitaka Fujii holds the record for the number of retractions of academic publications for a single author: 183 papers, or “roughly 7 percent of all retracted papers between 1980 and 2011”.
4. The chemistry of why bread stales, and how to slow retrogradation.

Mathematics and Mathematical Statistics Lesson of the Day – Convex Functions and Jensen’s Inequality

Consider a real-valued function that is continuous on the interval , where and are any 2 points in the domain of .  Let

be the midpoint of and .  Then, if

then is defined to be midpoint convex.

More generally, let’s consider any point within the interval .  We can denote this arbitrary point as

where .

Then, if

then is defined to be convex.  If

then is defined to be strictly convex.

There is a very elegant and powerful relationship about convex functions in mathematics and in mathematical statistics called Jensen’s inequality.  It states that, for any random variable with a finite expected value and for any convex function ,

.

A function is defined to be concave if is convex.  Thus, Jensen’s inequality can also be stated for concave functions.  For any random variable with a finite expected value and for any concave function ,

.

In future Statistics Lessons of the Day, I will prove Jensen’s inequality and discuss some of its implications in mathematical statistics.

Mathematical and Applied Statistics Lesson of the Day – The Motivation and Intuition Behind Chebyshev’s Inequality

In 2 recent Statistics Lessons of the Day, I

• introduced Markov’s inequality.
• explained the motivation and intuition behind Markov’s inequality.

Chebyshev’s inequality is just a special version of Markov’s inequality; thus, their motivations and intuitions are similar.

Markov’s inequality roughly says that a random variable is most frequently observed near its expected value, .  Remarkably, it quantifies just how often is far away from .  Chebyshev’s inequality goes one step further and quantifies that distance between and in terms of the number of standard deviations away from .  It roughly says that the probability of being standard deviations away from is at most .  Notice that this upper bound decreases as increases – confirming our intuition that it is highly improbable for to be far away from .

As with Markov’s inequality, Chebyshev’s inequality applies to any random variable , as long as and  are finite.  (Markov’s inequality requires only to be finite.)  This is quite a marvelous result!

Mathematical Statistics Lesson of the Day – Chebyshev’s Inequality

The variance of a random variable is just an expected value of a function of .  Specifically,

.

Let’s substitute into Markov’s inequality and see what happens.  For convenience and without loss of generality, I will replace the constant with another constant, .

Now, let’s substitute with , where is the standard deviation of .  (I can make this substitution, because is just another constant.)

This last inequality is known as Chebyshev’s inequality, and it is just a special version of Markov’s inequality.  In a later Statistics Lesson of the Day, I will discuss the motivation and intuition behind it.  (Hint: Read my earlier lesson on the motivation and intuition behind Markov’s inequality.)

Mathematical and Applied Statistics Lesson of the Day – The Motivation and Intuition Behind Markov’s Inequality

Markov’s inequality may seem like a rather arbitrary pair of mathematical expressions that are coincidentally related to each other by an inequality sign:

where .

However, there is a practical motivation behind Markov’s inequality, and it can be posed in the form of a simple question: How often is the random variable “far” away from its “centre” or “central value”?

Intuitively, the “central value” of is the value that of that is most commonly (or most frequently) observed.  Thus, as deviates farther and farther from its “central value”, we would expect those distant-from-the-centre values to be less frequently observed.

Recall that the expected value, , is a measure of the “centre” of .  Thus, we would expect that the probability of being very far away from is very low.  Indeed, Markov’s inequality rigorously confirms this intuition; here is its rough translation:

As becomes really far away from , the event becomes less probable.

You can confirm this by substituting several key values of .

 

• If , then ; this is the highest upper bound that  can get.  This makes intuitive sense;  is going to be frequently observed near its own expected value.

 

• If , then .  By Kolmogorov’s axioms of probability, any probability must be inclusively between and , so .  This makes intuitive sense; there is no possible way that can be bigger than positive infinity.

Mathematical Statistics Lesson of the Day – Markov’s Inequality

Markov’s inequality is an elegant and very useful inequality that relates the probability of an event concerning a non-negative random variable, , with the expected value of .  It states that

where .

I find Markov’s inequality to be beautiful for 2 reasons:

1. It applies to both continuous and discrete random variables.
2. It applies to any non-negative random variable from any distribution with a finite expected value.

In a later lesson, I will discuss the motivation and intuition behind Markov’s inequality, which has useful implications for understanding a data set.

Applied Statistics Lesson of the Day – The Coefficient of Variation

In my statistics classes, I learned to use the variance or the standard deviation to measure the variability or dispersion of a data set.  However, consider the following 2 hypothetical cases:

1. the standard deviation for the incomes of households in Canada is $2,000
2. the standard deviation for the incomes of the 5 major banks in Canada is $2,000

Even though this measure of dispersion has the same value for both sets of income data, $2,000 is a significant amount for a household, whereas $2,000 is not a lot of money for one of the “Big Five” banks.  Thus, the standard deviation alone does not give a fully accurate sense of the relative variability between the 2 data sets.  One way to overcome this limitation is to take the mean of the data sets into account.

A useful statistic for measuring the variability of a data set while scaling by the mean is the sample coefficient of variation:

where  is the sample standard deviation and is the sample mean.

Analogously, the coefficient of variation for a random variable is

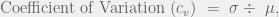
where is the random variable’s standard deviation and is the random variable’s expected value.

The coefficient of variation is a very useful statistic that I, unfortunately, never learned in my introductory statistics classes.  I hope that all new statistics students get to learn this alternative measure of dispersion.

Exploratory Data Analysis: Combining Histograms and Density Plots to Examine the Distribution of the Ozone Pollution Data from New York in R

Introduction

This is a follow-up post to my recent introduction of histograms.  Previously, I presented the conceptual foundations of histograms and used a histogram to approximate the distribution of the “Ozone” data from the built-in data set “airquality” in R.  Today, I will examine this distribution in more detail by overlaying the histogram with parametric and non-parametric kernel density plots.  I will finally answer the question that I have asked (and hinted to answer) several times: Are the “Ozone” data normally distributed, or is another distribution more suitable?

Read the rest of this post to learn how to combine histograms with density curves like this above plot!

This is another post in my continuing series on exploratory data analysis (EDA).  Previous posts in this series on EDA include

• Descriptive statistics
• Box plots
• The conceptual foundations of kernel density estimation
• How to construct kernel density plots and rug plots in R
• Violin plots
• The conceptual foundations of empirical cumulative distribution functions (CDFs)
• 2 ways of plotting empirical CDFs in R
• The conceptual foundations of histograms

Exploratory Data Analysis: Conceptual Foundations of Empirical Cumulative Distribution Functions

Introduction

Continuing my recent series on exploratory data analysis (EDA), this post focuses on the conceptual foundations of empirical cumulative distribution functions (CDFs); in a separate post, I will show how to plot them in R.  (Previous posts in this series include descriptive statistics, box plots, kernel density estimation, and violin plots.)

To give you a sense of what an empirical CDF looks like, here is an example created from 100 randomly generated numbers from the standard normal distribution.  The ecdf() function in R was used to generate this plot; the entire code is provided at the end of this post, but read my next post for more detail on how to generate plots of empirical CDFs in R.

Read to rest of this post to learn what an empirical CDF is and how to produce the above plot!